Artificial Intelligence: Search Methods
D. Kopec and T.A. Marsland
Introduction
Search is inherent to the problems and methods of artificial intelligence (AI). That is because AI problems are intrinsically complex. Efforts to solve problems with computers which humans can routinely solve by employing innate cognitive abilities, pattern recognition, perception and experience, invariably must turn to considerations of search. All search methods essentially fall into one of two categories 1) exhaustive (blind) methods and 2) heuristic or informed methods.
In this Chapter we will explore search methods in AI starting with blind exhaustive methods and then will turn to heuristic and optimal methods, including some more recent findings. The second half of the Chapter will focus on parallel methods.
The methods covered will include (for non-optimal, uninformed approaches) State-Space Search, Generate and Test, Means-ends Analysis, Problem Reduction, And/Or Trees, Depth First Search and Breadth First Search. Under the umbrella of heuristic (informed methods) are./ Hill Climbing, Best First Search, Bidirectional Search, The Branch and Bound Algorithm, and the Bandwidth Search . Tree Searching algorithms for games have proven to be a rich source of study and empirical data about heuristic methods. Methods covered include the minimax procedure, the alpha-beta algorithm, iterative deepening, the SSS* algorithm, and SCOUT.
Optimal methods covered include the A* algorithm, and the iterative deepening A* (IDA*) presented with an assortment of relatively recent parallel algorithms including the PIA* Algorithm, Parallel Iterative Deepening Algorithm (PIDA*), Parallel Window Search (PWS), Principal Variation Splitting Algorithm (PVS), and the Young Brothers Wait Concept.
1 Uninformed Search Methods
1.1 Search Strategies
All search methods in computer science share in common three necessities: 1) a world model or database of facts based on a choice of representation providing the current state, as well as other possible states and a goal state. 2) a set of operators which defines possible transformations of states and 3) a control strategy which determines how transformations amongst states are to take place by applying operators. Reasoning from a current state in search of a state which is closer to a goal state is known as
forward reasoning. Reasoning backwards to a current state from a goal state is known as backward reasoning. As such it is possible to make distinctions between bottom up and top down approaches to problem solving. Bottom up is often "goal directed" -- that is reasoning backwards from a goal state to solve intermediary sub-goal states. Top down or data-driven reasoning is based on simply being able to get to a state which is defined as closed to a goal state than the current state. Often application of operators to a problem state may not lead directly to a goal state and some backtracking may be necessary before a goal state can be found (Barr & Feigenbaum, 1981).1.2 State Space Search
Exhaustive search of a problem space (or search space) is often not feasible or practical due to the size of the problem space. In some instances it is however, necessary. More often, we are able to define a set of legal transformations of a state space (moves in the world of games) from which those that are more likely to bring us closer to a goal state are selected while others are never explored further. This technique in problem solving is known as
split and prune. In AI the technique that emulates split and prune is called generate and test. The basic method is:Repeat
Generate a candidate solution
Test the candidate solution
Until a satisfactory solution is found, or
no more candidate solutions can be generated:
If an acceptable solution is found, announce it;
Otherwise, announce failure.
Figure 1: Generate and Test Method
Good generators are complete, will eventually produce all possible solutions, and will not suggest redundant solutions. The are also informed; that is, they will employ additional information to limit the solutions they propose.
Means-ends analysis is another state space technique whose purpose is, given an initial state to reduce the difference (distance) between a current state and a goal state. Determining "distance" between any state and a goal state can be facilitated
difference-procedure tables which can effectively prescribe what the next state might be. To perform means-ends analysis:Repeat
Describe the current state, the goal state, and the difference between the two.
Use the difference between the current state and goal state, possibly with the description of the current state or goal state, to select a promising procedure.
Use the promising procedure and update the current state.
Until the GOAL is reached or no more procedures are available
If the GOAL is reached, announce success; otherwise, announce failure
.Figure 2: Means-Ends Analysis
The technique of problem reduction is another important approach to AI problems. That is, to solve a complex or larger problem, identify smaller manageable problems (or subgoals) that you know can be solved in fewer steps. steps.

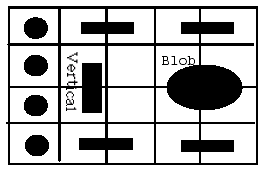
Figure 3: Problem Reduction and The Sliding Block Puzzle Donkey
This sliding block puzzle has been known for over 100 years. The object is to be able to bypass the Vertical bar with the Blob and place the Blob on the other side of the Vertical bar . The Blob occupies four spaces and needs two adjacent vertical or horizontal spaces in order to be able to move while the Vertical bar needs two adjacent empty vertical spaces to move left or right, or one empty space above or below it to move up or down. The Horizontal bars can move to any empty square to the left or right of them, or up or down if there are two empty spaces above or below them. Likewise, the circles can move to any empty space around them in a horizontal or vertical line. A relatively uninformed state space search can result in over 800 moves for this problem to be solved, with plenty of backtracking necessary. By problem reduction, resulting in the subgoal of trying the get the Blob on the two rows above or below the vertical bar, it is possible to solve this puzzle in just 82 moves!
Another example of a technique for problem reduction is called
And/Or Trees. Here the goal is to find a solution path to a given tree by applying the following rules:A node is solvable if --
1. it is a terminal node (a primitive problem),
2. it is a nonterminal node whose successors are AND nodes that are all solvable, OR
3. it is a nonterminal node whose successors are OR nodes and least one of them is solvable.
Similarly, a node is unsolvable if --
1. it is a nonterminal node that has no
successors )a nonprimitive problem to which no operator applies),2. it is a nonterminal node whose successors are AND nodes and at least one of them is unsolvable, or
3. it is a nonterminal node whose successors are OR nodes and all of them are unsolvable.
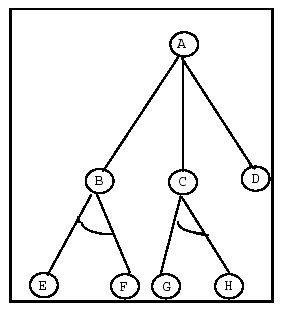
Figure 4: And/Or Tree
In this figure nodes B and C serve as exclusive parents to subproblems EF and GH respectively. One of viewing the tree is with nodes B, C, and D serving as individual, alternative subproblems . Solution paths would therefore be: {A-B-E}, {A-B-F}, {A-C-G}, {A-C-H}, and {A,D}.
In the special case where no AND nodes occur, we have the ordinary graph occurring in a state space search. However the presence of AND nodes distinguishes AND/OR Trees (or graphs) from ordinary state structures which call for their own specialized search techniques (Nilsson, 1971).
1.2.1 Depth First Search
The Depth First Search (DFS) is one of the most basic and fundamental Blind Search Algorithms. It is for those who want to probe deeply down a potential solution path in the hope that solutions do not lie too deeply down the tree. That is "DFS is a good idea when you are confident that all partial paths either reach dead emds or become complete paths after a reasonable number of steps. In contrast, "DFS is a bad idea if there are long paths, even infinitely long paths, that neither reacj dead emds nor become complete paths (Winston, 1992). To conduct a DFS:
(1) Put the Start Node on the list called OPEN.
(2) If OPEN is empty, exit with failure; otherwise continue.
(3) Remove the first node from OPEN and put it on a list called CLOSED.
Call this node n.
(4) If the depth of n equals the depth bound, go to (2);
Otherwise continue.
(5) Expand node n, generating all successors of n. Put these (in arbitrary order) at the beginning of OPEN and provide pointers back to n.
(6) If any of the successors are goal nodes, exit with the solution obtained by tracing back through the pointers; Otherwise go to (2).
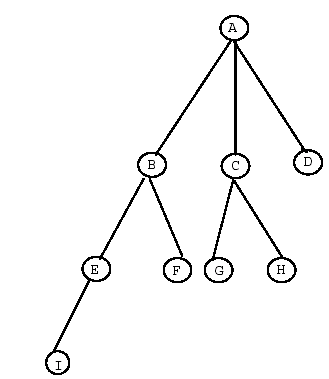
Figure 5: Tree Searching Example of Depth First Search and Breadth First Search
DFS always explores the deepest node first. That is, the one which is farthest down from the root of the tree. To prevent consideration of unacceptably long paths, a depth bound is often employed to limit the depth of search. DFS would explore the tree in Figure 5 in the order: A-B-E-I-F-C-G-H-D.
DFS with Iterative Deepening remedies many of the drawbacks of the DFS and the Breadth First Search. The idea is to perform a level by level DFS. It starts with a DFS with a depth bound of 1. If a goal is not found, then it performs a DFS with depth bound of 2. This continues, with the depth bound increasing by one with each iteration, although with each increase in depth the algorithm must re-perform its DFS to the prescribed bound. The idea of Iterative Deepening is credited to Slate and Adkin (1977) with their work on the Northwestern University Chess Program. Studies of its efficiency have been carried out by Korf (1985).
1.2.2 Breadth First Search
Breadth First Search always explores nodes closest to the root node first, thereby visiting all nodes of a given length first before moving to any longer paths. It pushes uniformly into the search tree. Breadth first search is most effective when all paths to a goal node are of uniform depth. It is a bad idea when the branching factor (average number of offspring for each node) is large or infinite. Breadth First Search is also to be preferred over DFS if you are worried that there may be long paths (or even infinitely long paths) that neither reach dead ends or become complete paths (Winston, 1992). For the tree in Figure 5 Breadth First Search would proceed alphabetically.
The algorithm for Breadth First Tree Search is:
(
1) Put the start node on a list called OPEN.(2) If OPEN is empty, exit with failure;
Otherwise continue.
(3) Remove the first node on OPEN and put it on a list called CLOSED;
Call this node n;
(4) Expand node n, generating all of its successors. If there are no successors, go immediately to (2).
Put the successors at the end of OPEN and provdie pointers from these successors back to n.
(5) If any of the successors are goal nodes, exit with the solution obtained by tracing back through the pointers; Otherwise go to (2)
1.3.3 Bidirectional Search
To this point all search algorithms discussed (with the exception of means-ends analysis and backtracking) have been based on forward reasoning. Searching backwards from goal nodes to predecessors is relatively easy. Pohl (1969, 1971) combined forward and backward reasoning into a technique called bidirectional search. The idea is to replace a single search graph, which is likely to grow exponentially, with two smaller graphs -- one starting from the initial state and one starting from the goal. The search is approximated to terminate when the two graphs intersect This algorithm is guaranteed to find the shortest solution path through a general state-space graph. Empirical data for randomly generated graphs showed the Pohl's algorithm expanded only about 1/4 as many nodes as unidirectional search (Barr and Feigenbaum, 1981). Pohl also implemented heuristic versions of this algorithm.
2 Heuristic Search Methods
George Polya, via his wonderful book "How To Solve It" (1945) may be regarded as the "father of heuristics". In essence Polya's effort focused on problem-solving, thinking and learning. He developed a short "heuristic Dictionary" of heuristic primitives. Polya's approach was both practical and experimental. He sought to develop commonalities in the problem solving process through the formalization of observation and experience.
Present-day researches notions of heuristics are somewhat distant from Polya's (Bolc and Cytowski, 1992). Tendencies are to seek formal and rigid algorithmic solutions to specific problem domains rather than the development of general approaches which could be appropriately selected and applied for specific problems.
The goal of a heuristic search is to reduce the number of nodes searched in seeking a goal. In other words, problems which grow combinatorially large may be approached. Through knowledge, information, rules, insights, analogies, and simplification in addition to a host of other techniques heuristic search aims to reduce the number of objects examined. Heuristics do not guarantee the achievement of a solution, although good heuristics should facilitate this. Heuristic search is defined by authors in many different ways:
•
it is a practical strategy increasing the effectiveness of complex problem solving (Feigenbaum, Feldman, 1963)•
it leads to a solution along the most probable path, omitting the least promising ones (Amarel, 1968)•
it should enable one to avoid the examination of dead ends, and to use already gathered data (Lenat, 1983) .The points at which heuristic information can be applied in a search include:
1. deciding which node to expand next, instead of doing the expansions in a strictly breadth-first 0r depth-first order;
2. in the course of expanding a node, deciding which successor or successors to generate -- instead of blindly generating all possible successors at one time, and
3. deciding that certain nodes should be discarded, or pruned, from the search tree.
Bolc and Cytowski (1992) add:
... use of heuristics in the solution construction process increases the uncertainty of arriving at a result ... due to the use of informal knowledge (rules, laws, intuition, etc.) whose usefulness have never been fully proven. Because of this, heuristic methods are employed in cases where algorithms give unsatisfactory results or do not guarantee to give any results. They are particularly important in solving very complex problems (where an accurate algorithm fails), especially in speech and image recognition, robotics and game strategy construction. ...
Heuristic methods allow us to exploit uncertain and imprecise data in a natural way. ... The Main objective of heuristics is to aid and improve the effectiveness of an algorithm solving a problem. Most important is the elimination from furhter consideration of some subsets of objects still not examined. ..."
Most modern heuristic search methods are expected to bridge the gap between the completeness of algorithms and their optimal complexity (Romanycia and Pelletier, 1985). Strategies are being modified in order to arrive at a quasi-optimal -- instead of an optimal -- solution with a significant cost reduction (Pearl, 1984).
Games, especially two-person, zero-sum games of perfect information like chess and checkers have proven to be a very promising domain for studying and testing heuristics.
2.1 Hill Climbing
Hill climbing is a depth first search with a heuristic measurement that orders choices as nodes are expanded. The heuristic measurement is the estimated remaining distance to the goal. The effectiveness of hill climbing is completely dependent upon the accuracy of the heuristic measurement.
To conduct a hill climbing search:
Form a one-element queue consisting of a zero-length path that contains only the root node.
Repeat
Remove the first path from the queue; create new paths by extending the first path to all the neighbors of the terminal node.
Reject all new paths with loops.
Sort the new paths, if any, by the estimated distances between their terminal nodes and the goal.
Until the first path in the queue terminates at the goal node or the queue is empty
If the goal node is found, announce success, otherwise announce failure.
Winston (1992) lucidly explains the potential problems affecting hill climbing. They are all related to issue of local "vision" versus global vision of the search space. The foothills problem is particularly subject to local maxima where global ones are sought, while the plateau problem occurs when the heuristic measure does not hint towards any significant gradient of proximity to a goal. The ridge problem illustrates just what it's called: you may get the impression that the search is taking you closer to a goal state, when in fact you travelling along a ridge which prevents you from actually attaining your goal.
2.2 Best First Search
Best first search is a general algorithm for heuristically searching any state space graph. It is equally applicable to data and goal driven searchers and supports a variety of heuristic evaluation functions. Best first search can be used with a variety of heuristics, ranging from a state's "goodness"
to sophisticated measures based on the probability of a state leading to a goal which can be illustrated by examples of Bayesian statistical measures.
Similar to the DFS and breadth first search algorithms, the best-first search uses lists to maintain states: OPEN to keep track of the current fringe of the search and CLOSED to record states already visited. In addition the algorithm orders states on OPEN according to some heuristic estimate of their "closeness" to a goal. Thus, each iteration of the loop considers the most "promising" state on the OPEN list. (Lugar and Stubblefield, 1993) Just where hill climbing fails, its short-sighted, local vision, is where the Best First Search improves. The following description of the algorithm closely follows that of Lugar and Stubblefield (1993, p121):
At each iteration, Best First Search removes the first element from the OPEN list. If it meets the goal conditions, the algorithm returns the solution path that led to the goal. Each state retains ancestor information to allow the algorithm to return the final solution path.
If the first element on OPEN is not a goal, the algorithm generates it descentdants. If a child state is already on OPEN or CLOSED, the algorithm checks to make sure that the state records the short of the two partial solution paths. Duplicate states are not retained. By updating the ancestor history of nodes on OPEN and CLOSED, when they are rediscovered, the algorithm is more likely to find a shorter path to a goal.
Best First Search then heuristically evaluates the states on OPEN, and the list is sorted according to the heuristic values. This brings the "best" state to the front of OPEN. It is noteworthy that these estimates are heuristic in nature and therefore the next state to be examined may be from any level of the state space. OPEN, when maintained as a sorted list, is often referred to as a priority queue.
Here is a procedure for Best First Search:
Procedure Best_First_Search;

Figure 6: The Best First Search Algorithm
Figure 7 is reproduced below (with permission) from Lugar and Stubblefield (1993, p121-22). Much of the fourth chapter of their excellent text is devoted to the Best First Search
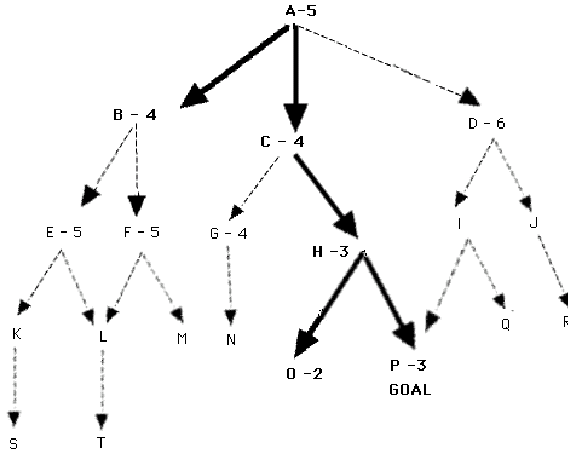
We provide their description below: Figure 7 shows a hypothetical state space with heuristic evaluations attached to some of its states. The states with attached evaluations are those actually generated in best-first search. The states expanded by the heuristic search algorithm are indicated in
BOLD; note that it does not search all of the space. The goal of best-first search is to find the goal state by looking at as few states as possible; the more informed the heuristic, the fewer states are processed in finding the goal.A trace of the execution of Procedure
Best_First_Search appears below. P is the goal state in this example. States along the path to P tend to have low heuristic values. The heuristic is fallible: the state O has a lower value than the goal itself and is examined first. Unlike hill climbing, the algorithm recovers from this error and finds the correct goal.1. Open = {A5}; Closed = { }
2. evaluate A5; Open = {B4, C4, D6}; Closed = {A5}
3. evaluate B4; Open = {C4, E5, F5, D6}; Closed = {B4, A5}
4. evaluate C4; Open = {H3, G4, E5, F5, D6}; Closed = {C4, B4, A5}
5. evaluate H3; Open = {O2, P3, G4, E5, F5, D6}; Closed = {H3, C4, B4, A5}
6. evaluate O2; Open = {P3,G4,E5, F5, D6}; Closed = {O2, H3, C4, B4, A5}
7. evaluate P3; the solution is found!
The Best First Search algorithm always selects the most promising state on Open for further expansion. Even though the heuristic it is using for measurement of distance from the goal state may prove erroneous, it does not abandon all the other states and maintains them on Open. If the algorithm leads search down an incorrect path, it will retrieve some previously generated "next best" state from Open and shift its focus to another part of the space. In the example above children of State B were found to have poor heuristic evaluations, and hence the search shifted to state C. However the children of B were kept on Open and returned to later.
Defining Terms
Admissibility Condition
A* Algorithm
Alpha - Beta
And/Or Tree: A tree which enables the expression of the decomposition of a problem into subproblems allowing alternate solutions to problems and subproblems through the use of AND/OR node labelling schemes.
Backtracking : A component process of many search techniques whereby recovery from unfruitful paths is sought by backing up to a juncture where new paths can be explored.
Bandwidth Search
Best First Search (BFS) : A heuristic search technique which finds the most promising node to explore next by maintaining and exploring an ordered Open node list.
Bidirectional Search: A search algorithm which replaces a single search graph, which is likely to with two smaller graphs -- one starting from the initial state and one starting from the goal state.
Blind Search : A characterization of all search techniques which are heuristically uninformed. Included amongst these would normally be state space search, means ends analysis, generate and test, depth first search, and breadth first search amongst others.
Branch and Bound Algorithm
Breadth First Search: An uninformed search technique which proceeds level by level visiting all the nodes at each level (closest to the root node) before proceeding to the next level.
Conspiracy Numbers (McAllester, 1988)
Depth First Search (DFS): A search technique which visits each node as deeply (as far away from the root node) down to the left as possible
Generate and Test: A search technique which proposes possible solutions and then tests them for their feasibility
Heuristic Search: an informed method of searching a state space with the purpose of reducing its size and finding one or more suitable goal states.
Iterative Deepening Algorithm (IDA*)
Means-Ends Analysis: An AI technique which tries to reduce the "difference" between a current state and a goal state.
SCOUT
SSS*
PIA* (Huang & Davis, 1989)
Parallel Iterative Deepening Algorithm (PIDA*) (Rao, et. al, 1987)
Parallel Window Search (PWS) (Baudet, 1978)
Mandatory Work First (Akl et. al, 1982)
PVSplit (Principal Variation Split (Marsland and Campbell, 1982)
Young Brothers Wait Concept (Feldman, 1993)
Additional Necesary Refs.
Feigenbaum, E , Feldman, J., Computers and Thought New York: McGraw-Hill, 1963.
Amarel, S. On representation of problems of reasoning about actions. Machine Intelligence, 1968, No 3, pp131-171.
Lenat, D. (1983) Theory formation by heuristic search. In: Search and Heuristics, J. Pearl (Ed.) New York: , North Holland, 1983.
Romanycia, M, Pelletier, F. What is heuristic? Computer Intelligence, 1985, No. 1, pp. 24-36.