CISC 3620 Chapter 2

CISC 3620
Computer Graphics
Chapter 2

Two-D Applications

Special case of 3D (z coordinate is always 0)

A First OpenGL Program - The Sierpinski Gasket

Three non collinear points (x₁, y₁, 0), (x₂, y₂, 0), (x₃, y₃, 0)) form a triangle on the z-plane.
To construct the desired image:
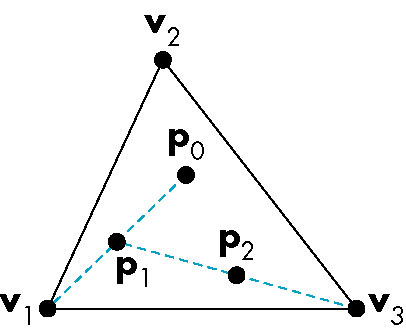
1. Pick an initial point (x, y, 0)
2. Randomly select one of the three vertices of the triangle
3. Find the midpoint between the selected vertex and the initial point
4. Display the midpoint
5. Set the initial point to the midpoint
6. Go to step 2

As code:

gasket(Point v1, Point v2, Point v3) {
   const int NUM_POINTS = however many points we want to generate
   Point p = random point inside triangle formed by v1, v2, v3
		
   for (int i = 1; i < NUM_POINTS; i++) {
      Point aRandomVertex = randomly choose one of v1, v2, v3
      Point midPoint = calculate the midpoint of aRandomVertex and p
      display(midpoint)
      p = midpoint
   }
}

Moving to an Actual Implementation

Vertex specification
Color specification
Size and position of the image
Window creation
Maintenance of the display

A C++/OpenGL Implementation of the Above

 1. #define GLUT_DISABLE_ATEXIT_HACK
 2. #include <windows.h>

 3. #include <GL/gl.h>
 4. #include <GL/glut.h>
 5. #include <stdlib.h>

 6. static void display(void) {

 7.     GLint vx[] = {100, 0, 200};
 8.     GLint vy[] = {0, 200, 200};

 9.     GLint px = 100;
10.     GLint py = 100;

11.     glClear(GL_COLOR_BUFFER_BIT);
12.     glColor3f(1.0, 0.0, 0.0);

13.     glBegin(GL_POINTS);
14.         for (GLint i = 0; i < 10000; i++) {
15.             int whichV = rand() % 3;
16.             int newPx = (px + vx[whichV]) / 2;
17.             int newPy = (py + vy[whichV]) / 2;
18.             glVertex2i(newPx, newPy);
19.             px = newPx;
20.             py = newPy;
21.         }
22.     glEnd();
23.     glFlush();
24. }
 
25. void init() {
26.     glClearColor(1.0, 1.0, 1.0, 1.0);
27.     gluOrtho2D(0, 500, 500, 0);
28. }

29. int main(int argc, char *argv[]) {
30.     glutInit(&argc, argv);
31.     glutInitWindowPosition(100, 100);
32.     glutInitWindowSize(500, 500);
33.     glutCreateWindow("Gasket");
 
34.     glutDisplayFunc(display);
 
35.     init();

36.     glutMainLoop();

37.     return 0;

38. }

A 'Thirty-Second' Overview of the Above

The Program Structure

Consists of:
- the usual main function (this is C++ after all)
- a graphics initialization function init (my choice of function name)
- display function, display (my choice of function name)

The Program's Excution Lifecycle

The graphics system is initialized (30)
A window is specified and created (31-33)
A display callback function is specified (6-24) and registered (34)
Other app-specific initialization is specified (25-28) and called (35)
OpenGL is left to its own devices (36)
When OpenGL is done (window is closed), the program exits (37)

Vertices

vertex - position in n-dimensional space
specified by n values -- one per dimension
- We'll be restricting ourselves to 2, 3, and 4-dimensional spaces
Used to specify the geomtric primitives points, lines, polygons, etc
Note that vertex and point are somewhat different
- vertex is a position specification; point is a geometric object
- a point is specified by a single vertex

The OpenGL `GLVertex` Function

GLVertex<n><t>[v] n -- dimensions: 2, 3, or 4 t -- type: i integer f float d double In addition, there are corresponding OpenGL types, such as GLfloat and GLint, The OpenGL types are preferred because they aid in providing portability across platforms, or ease of changing representation v -- allows specification of the vertices using an array (vector) Useful for declaring and working with point data types Each point represented as an array of n coordinates-- one per dimension We'll reimplement the gasket program in this manner below





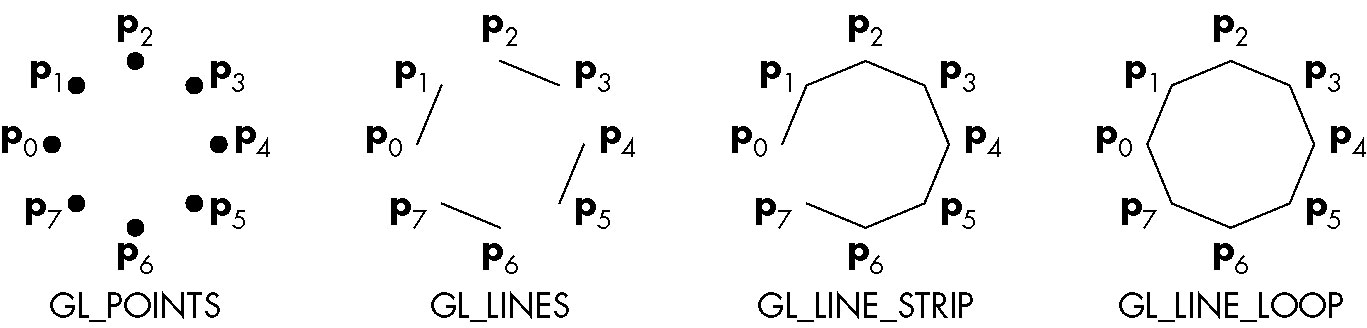
Specifying an Object as a Sequence of Vertices

	The vertices of a single geometric object is nested between the pair of GLOpen functions GLBegin
					and GLEnd
	
GLBegin takes as an argument the manner in which the specified vertices are, i.e., the sort of object they specify:
	
		 
		 		
					GL_POINTS 	 Vertices form individual points
		 		

					GL_LINES 		 Vertices form pairwise line segments
		 		

					GL_LINE_STRIP	 Adjacent vertices are connected (polyline)
		 		

					GL_LINE_LOOP		 Same as LINE_STRIP, but sequence is closed-- i.e., last and first vertices are connected		
		 		

		 
		 


		 
		 
		 
Basic Structure of an OpenGL Program


		Create window (platform specific)
		
Define and register display callback function
		
Define and register other callback functions and registrations (keyboard and mouse events, window resizing)


The Graphics Systems vs User Interaction

	The actual graphics system is platform independent
	
User interaction (window management, user input) is platform-dependent


The Display Callback Function


		We'll talk more about this in Chapter 3
		
For the moment, we'll simply say that the function named in glutDisplayFunc is
					called everytime there is a need to redisplay the OpenGL window.


Coordinate Systems

		Device independent coordinates allows programmer to ignore
							issues related to the particular input/output device being used.
			
					World coordinates, object coordinates
					
May be represented using floating point values
			 
		
Device coordinates, window coordinates,
						screen coordinates
			
				Correspond to actual device
				
Represented using integers
			
		
Mapping of device-independent to device coordinates

		

			
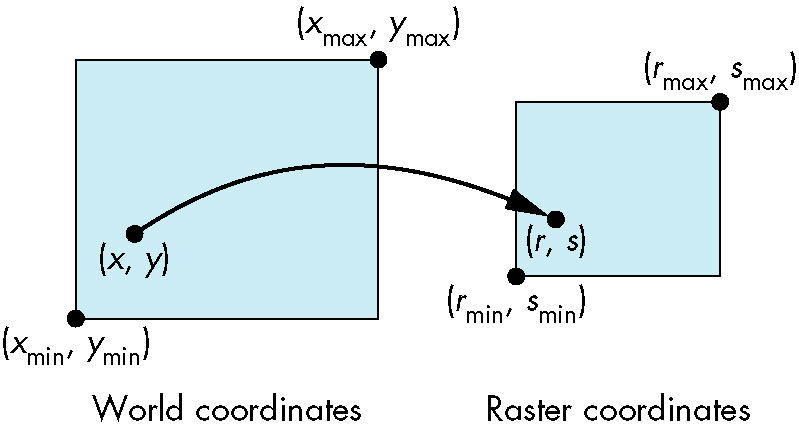
				One of the tasks of the graphics system 
			
	
		
OpenGL API

Major Categories of OpenGL's Functions


  Primitive functions
  	
			Low-level graphic objects: points, lines, polygons...
		
  
Attribute functions
		
			Control how a primitive is displayed: color, thickness
		Viewing functions
		
			how the camera sees the graphics 'universe'
		
  
Transformation functions
		
			Provides ability to transform the object: scaling, translation, rotation
		
  
Input functions
		
			Handles user input
		
  
Control functions
		
			Window management, error handling, initialization
		
  
Query functions
		
			Obtain information about the graphics environment
		


(Finite) State Machines


		A theoretical model of a machine that has a fixed number of states and changes its state
					based upon input.
		
The change of state is known as a transition
		
There is usually an initial state
		
Machine stays in same state until explicitly changed-- i.e., it is persistent
		
OpenGL may be thought of as implementing a state machine
			
					-- changes to its state (e.g. setting the pen color) persist until changed
			  



OpenGL Interface




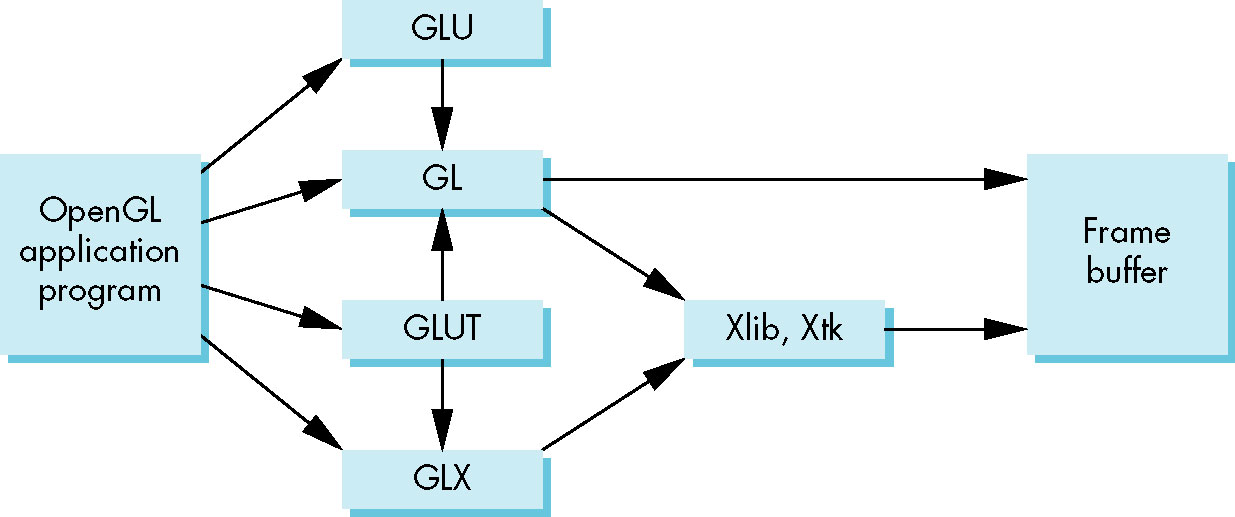
		Main OpenGL library (GL)
			
				gl function prefix
			
		
OpenGL Utility Library (GLU) 
			
				Convenience functions
				
Uses GL functions only
				
glu function prefix
			
		
GLX (unix), wgl (windows), agl (Mac)
			
				Windowing system (platform specific)
			 
		
OpenGL Utility Toolkit (GLUT) 
			
				common denominator of windowing/user-interaction functionality
				
cross-platform
				
event-driven
				
windows, mouse, keyboard, not much more
			

			
			
Primitives

		Geometric objects
			
				Specified as set of vertices
				
Formal specification -- can be transformed
			
			glBegin(type);
   glVertex*(...);
	 ...
   glVertex*(...);
glEnd();
			
		
Image/raster primitives
			
				Essentially arrays of pixels
				
Cannot be manipulated like geometric objects
				
Separate pipeline
			

	


Polygons




Rendering/filling polygons quickly require that they have well-defined interiors: simple,
		convex, and flat.									

	Simple
		
			No edges intersect 
		
		
	
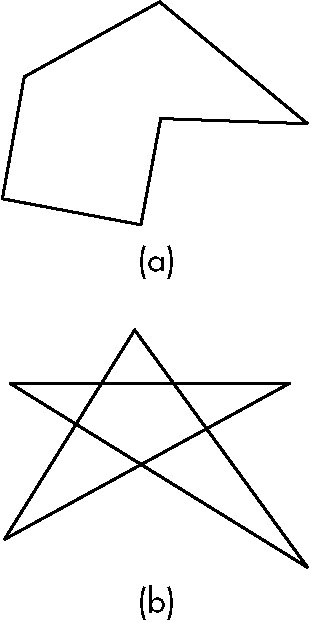
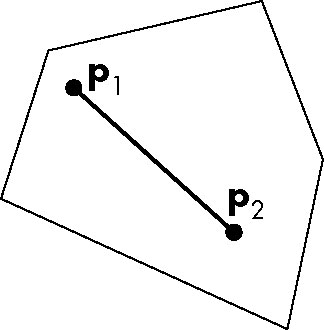
Convex
		
			Given two points within the objects, the line segment between them lies
						entirely within the object 
		
		
		

	
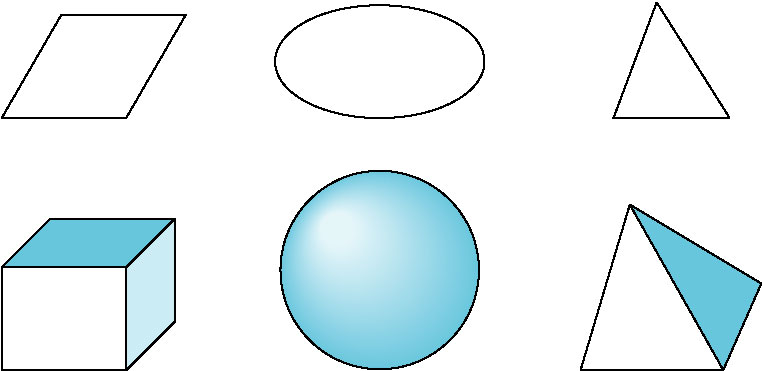
In three dimensions, using triangles (which must always lie in a single plane, and thus are always flat) 
				 makes rendering efficient and correct.
		

Polygons in OpenGL


	GL_POLYGON
		
				Similar to LINE_LOOP but defines an interior (that can be filled) as well
		
	
GL_TRIANGLES, GL_QUADS

		
		
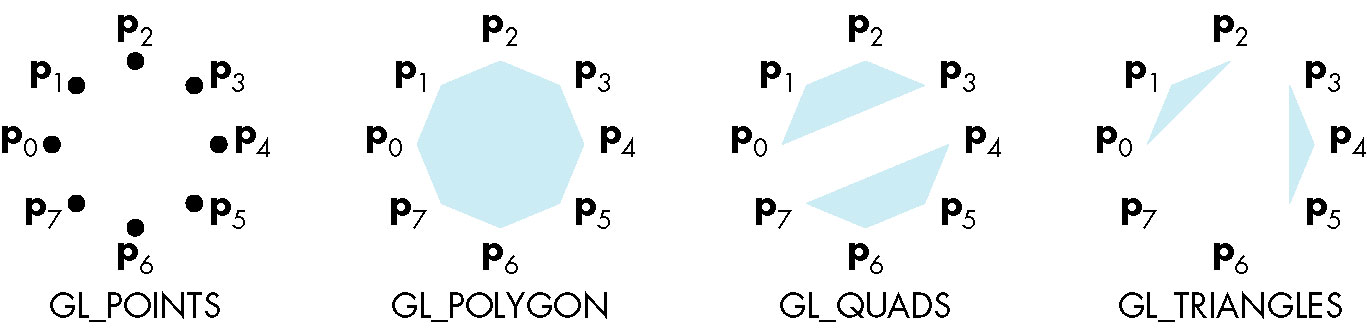
				Convenience (and possible optimization) types of GL_POLYGON
		
	
GL_TRIANGLE_STRIP, GL_QUAD_STRIP, GL_TRIANGLE_FAN

		

		
			Provides ability to form triangles or quadrilaterals that share vertices
				 
				 		GL_TRIANGLE_STRIP
							
								Each additional vertex combines with previous two to form a new triangle
							
						
GL_QUAD_STRIP
							
								Each additional two vertices combines with previous two to form a new quadrilateral
							
				 		
GL_TRIANGLE_FAN
							
								Initial fixed point. First pair of additional vertices forms first triangle. Each additional
											vertex combines with previous and fixed point to form additional triangles.
							
					
		
	
	
Approximating a Sphere


	An application of using quad strips and triangle fans
	
Subdivide surface of sphere into longitudinal and latitudinal lines (circles)

		

	
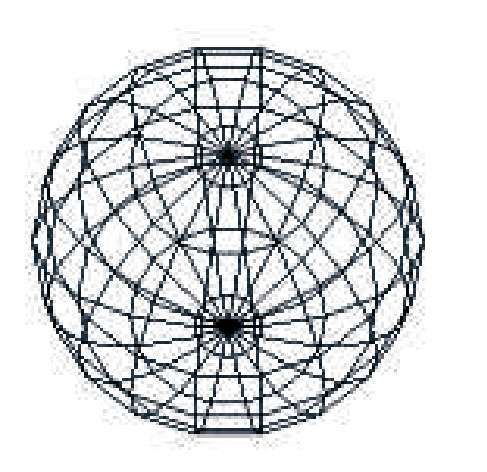
The above form a grid of quadrilaterals which we can create using QUAD_STRIPS
	
At the poles, we use TRIANGLE_FANS to finish off the top and bottom of the sphere

	
Text


		Nongraphical systems uses a hardware character generator (similar in concept to
					raster text described below).
		
Two basic ways of forming text
			
					raster - character is formed from a matrix of bits known as a bit block
						
								Fast transfer of characters into frame buffer (bitblt - bit block transfer)
								
Scaling or replicating issues
						
					
stroke
						
								Character is formed using vertices 
								
No different than any other geometric object
									
										All the usual operation may be performed on them: filling, transformations (e.g., rotation)
									
						
					
Above two are analogous to vector vs raster displays
			


Curved Objects


	Various approaches
		
    	Can approximate them
    		
    			e.g. circle using n-gon; spehere using quad and tirangles
    			
In general, approximate a curved surface using a mesh of (convex) polygons
    				
    					This is called a tessellation
						
					
			
Can use graphical function to graph the mathematical definition of a curved surface
				
					Use the definition to determine the defining vertices
						
							e.g. circle is defined via a center and a single point on circumfrence; then use mathematical
											definition to draw the circle
						
				
		
							 
						 
Attributes


		We've been looking at primitives -- geomtric objects, text, ...
		
Attributes describe how a primitive gets rendered
			
				Primitives are the nouns, attributes are the adjectives
				
Color, line style, ...
						 
						 		 size of text vs height/width of geometric object
						 
			
		
Immediate mode - object is rendered (sent to frame buffer) as soon as possible.
			
					Current state of attributes associated with object's type are applied
					
Object's specs are not stored anywhere in system
					
When display is cleared, objec'ts image disappears as well
					
Contrasted with use of a display file/list which maitains 
								object information
							
									Shapes in Paint vs shapes in Word
							
			


Color

		

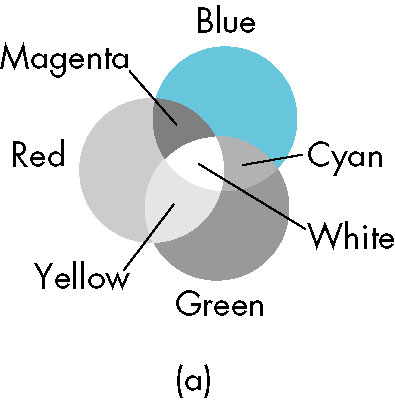
		Additive color 
			
					Three primary colors are added to form desired color
					
Light is added to black to produce color
					
Primaries are usually red, green, blue (RGB)
			
		

		
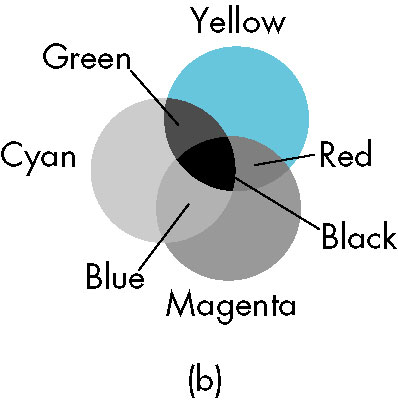
Subtractive color 
			
					Primary colors in the form of pigments remove color from white to form desired color
					
Primaries are usually cyan, magenta, yellow (CMY)
			
		

		
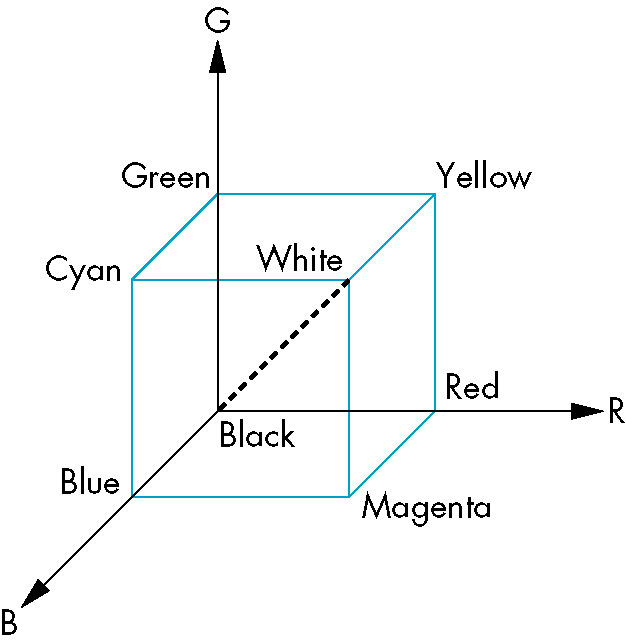
color solid/cube
				
					R, G, B axes
					
Origin at 0, opposite corner at (1, 1, 1)
					
0 represents absence; 1 represents saturation
					
Vertices correspond to primaries and complementaries
					
(0, 0, 0) - (1, 1, 1) diagonal represents grey shades
				


RGB Color Model

	Each pixel has a individual red, green, and blue components
		
				Separate buffer in frame buffer for each color component
		
	
Programmer specifies value of each component
			
					Typically using the color cube
			
	
In OpenGL
								 glColor3f(1.0, 0.0, 0.0);		 // red -- state of system changed until next color change
							 	
		
			Can add a fourth dimensional parameter known as alpha
				
					Can be used to specify opacity/transparency
						
								complementary terms - spectrum of value
								
1.0 completely opaque
								
0.0 completly transparent
						
								 glColor4f(1.0, 0.0, 0.0, 1.0);		 // opaque red
							 	
				
	

		 
		
Indexed Color Model

	Used in earlier systems with limited buffer memory (particularly wrt color depth)
	
Dividing the buffer depth (e.g. 8 bits) into R,G,B components (2 or 3 bits per component produces
							very limited color expressivity)
	
Rather, use the depth as an index into a color lookup table of full (24 bit) color whose
							size is 2^depth elements

			
			

	
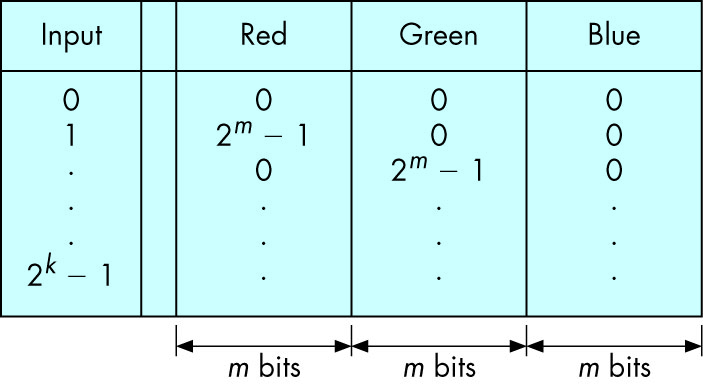
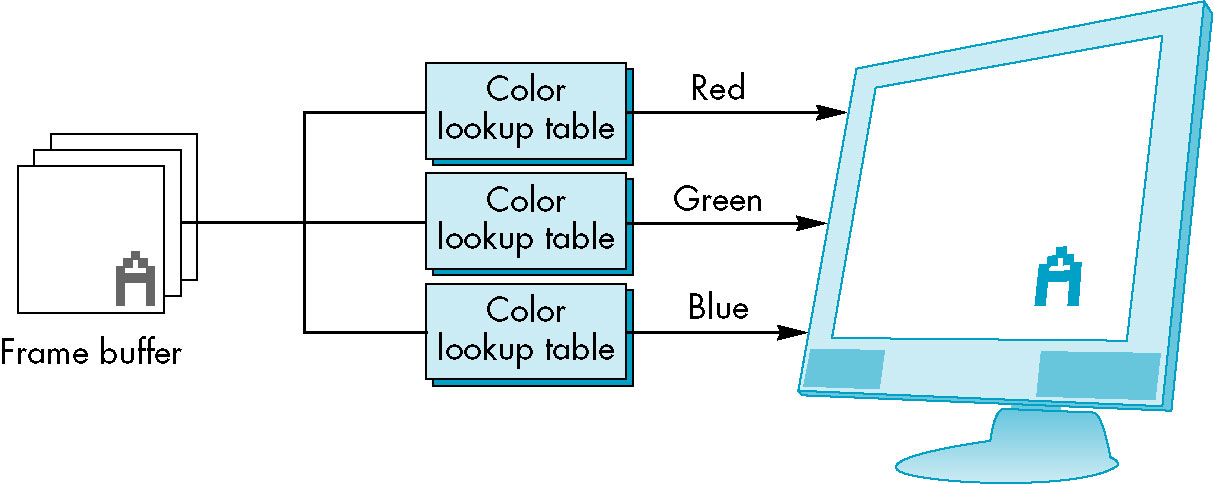
This limits the number of colors that can be used (simultaneously), but each color can be full 24 bit
	
With current low cost of memory and large buffers, no longer really necessary
		 

Setting Color Attributes

		glClearColor((R, G, B, A) - Sets the clear (background) color
		
glColornt(...) - Sets the color
		
glPointSize(double size) - Sets the point size and line width (in pixels)
			
				Why a double? -- what does a non-integer point size mean? 
			
		 

Viewing

	Camera position determines
		
			which objects in system are visible
			
how those objects appear
		


Orthographic Viewing


	Default (and simplest) in OpenGL
	
Inspired by synthetic camera model placed infinitely far from objects
		
    	Lines of projection (projectors) become parallel
    	
Center of projection becomes direction of projection
    
    
	
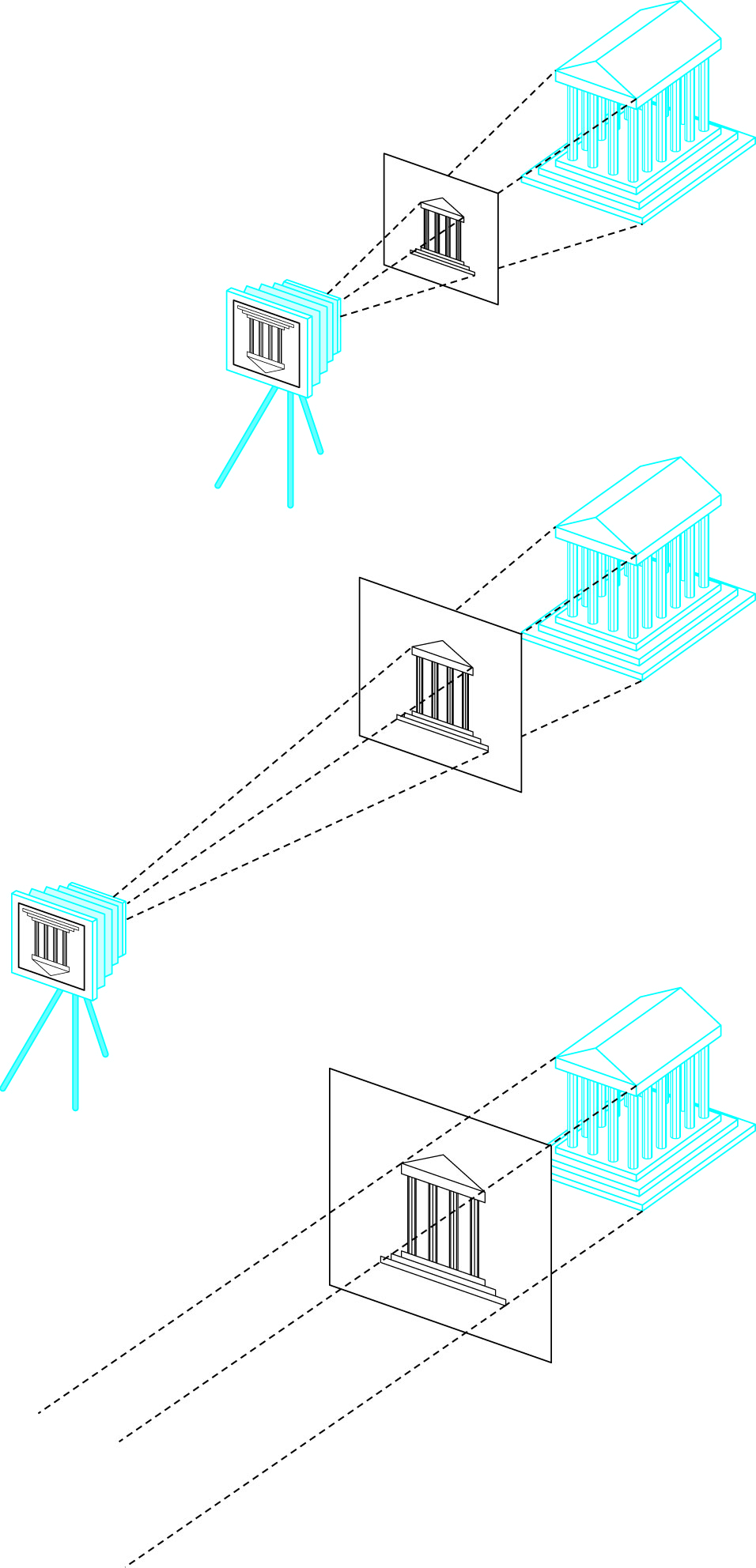
We'll simply constrain
		
			our projectors to be parallel to z axis
			
have projection plane be placed at z = 0 
			
Sliding the plane along the z axis, has no change on where projectors intersect the plane
		
    
	
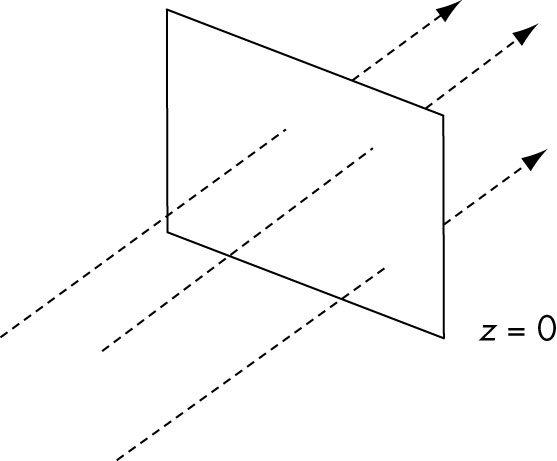
We'll specify a point in the projection plane from which we
		
				measure a view volume
				
specify a direction of projection
		


Orthographic Viewing in OpenGL


  OpenGL defaults to a center at origin and direction facing the negative z axis

      
  	
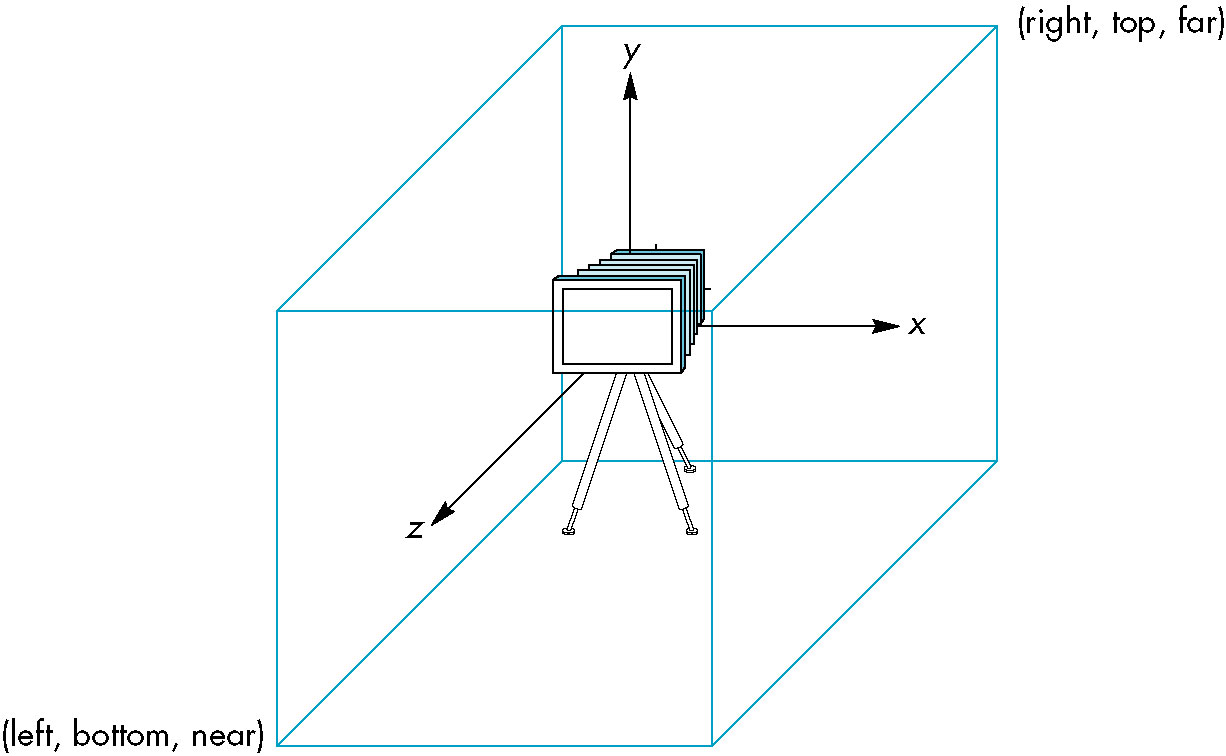
  		Points are projected from (x, y, z) to (x, y, 0)

      
			
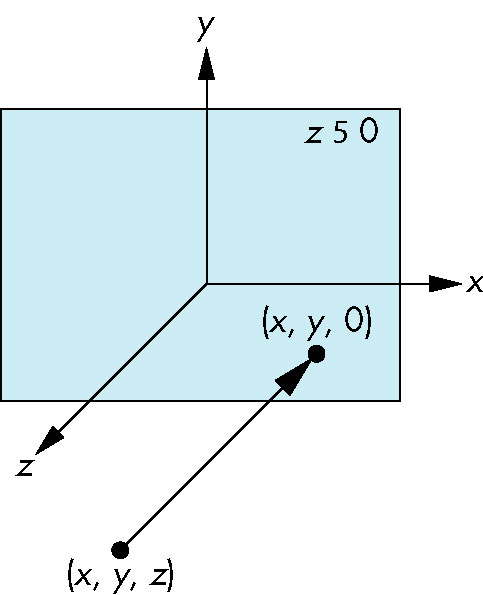
This 'camera' can see behind itself
				
						Any point within the viewing volume is projected 
				
		
	
Functions for ortho viewing
		
    	glOrtho(left, right, bottom, top, near, far)

			      
				
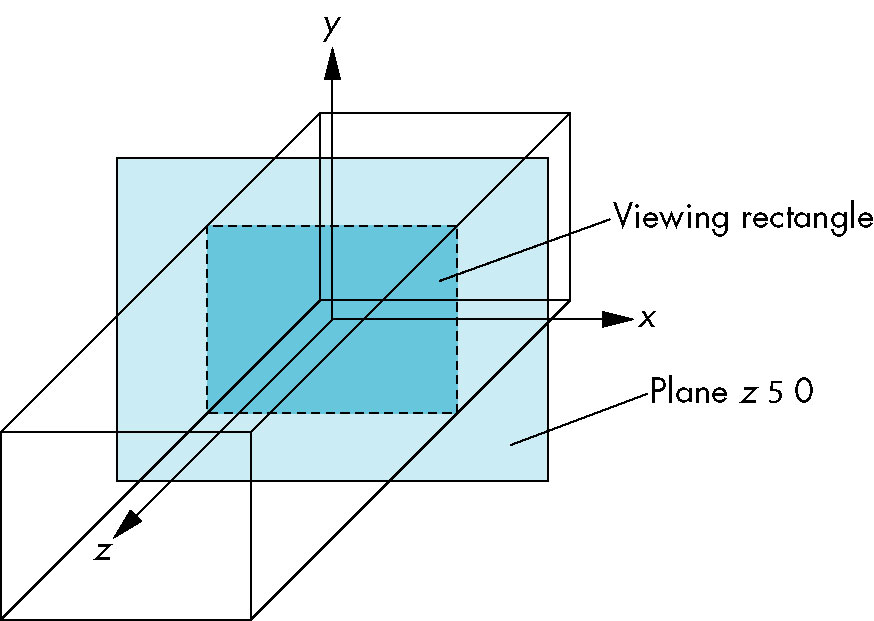
					Default is a 2 x 2 x 2 cube with (-1.0, -1.0, -1.0) lower left corner behind and (1.0, 1.0, 1.0) upper right in front.
				
			
All distances are from the camera
    	
gluOrtho2D(left, right, bottom, top) --- sets near/far to -1.0/1.0
		


Matrix Modes


	Tranformations on the image and view is performed by applying transformation matrices.
	
Some of these are applied to objects and their view (model-view matrix) and others to modify 
					 the viewing volume (projection matrix)
		
			These both default to an intiial identity matrix
		
	
At any one point the state of the system contains which matrix is being modified by application of transformations. 
		
				This is known as the matrix mode
				
The default in OpenGL is the model-view
				

		 
	
Typical code to set a 2-dimensional viewing volume:
	glMatrixMode(GL_PROJECTION);							// Switch to the desired mode
glLoadIdentity();													// Clear back to an identitiy matrix
gluOrtho2d(0, 50, 0, 50);									// Apply the transformation
glMatrixMode(GL_MODELVIEW);								// Leave it in a known mmode
	


Aspect Ratio and Viewports

	aspect ratio - ration of width to height
	
Can get distortion if glOrtho and glutInitWindowSize don't have
					same aspect ratio.

			      
	
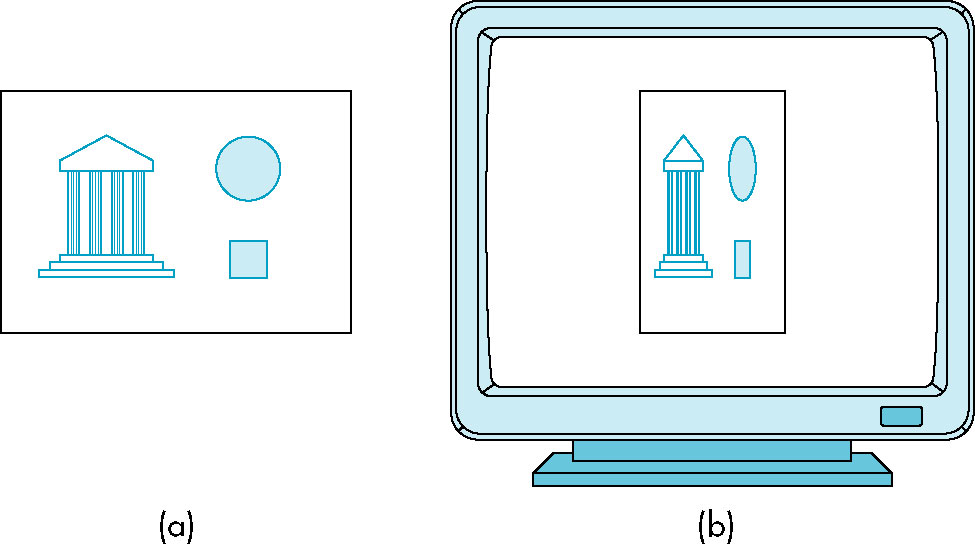
Can either:
		
			ensure that window and viewing rectangle have same ration, or
			
Use glViewport(x, y, width, height) function to specify
							a subarea of display window (x, y are relative to the window's
							coordinate system)

	      
			
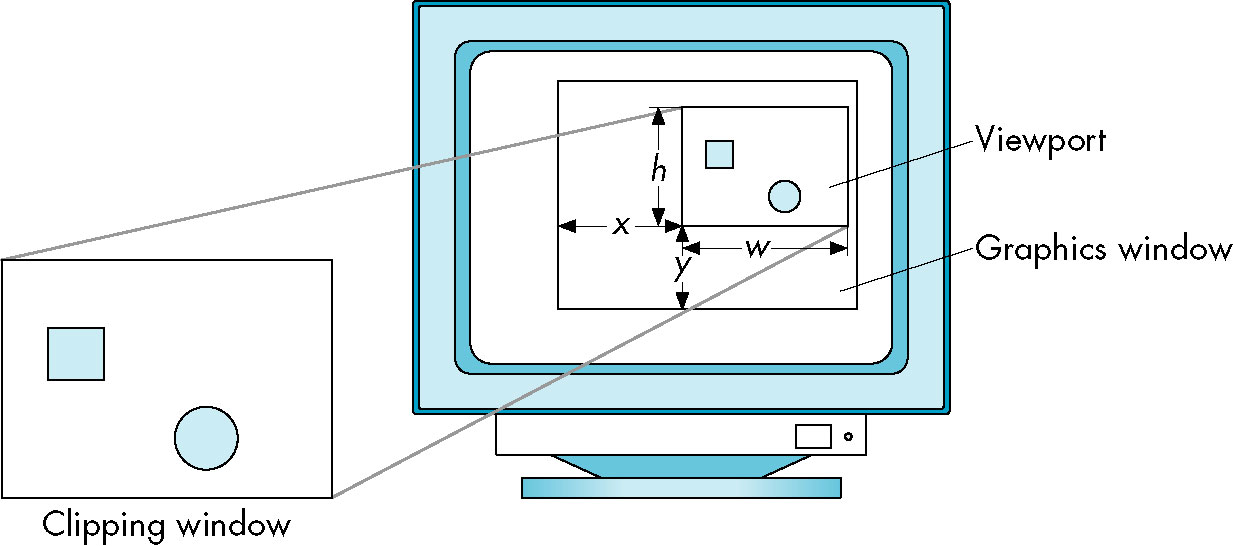
Changing the viewport achieves the effect of multiple views within the same window.
		


Revisiting the Gasket


	Another algorithm for construction of the gasket
		
			Connect the midpoints of the initial triangle, forming four triangles

			     
			
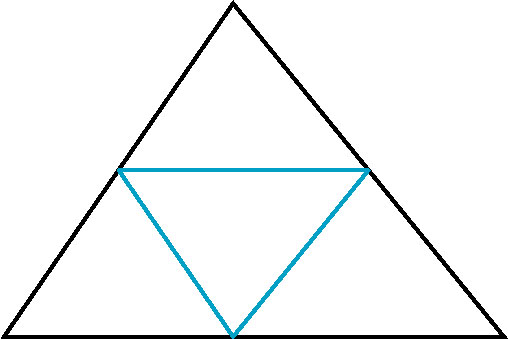
Repeat the process recursively on the outer triangles, for desired level of division
			
When terminating the recursion draw the outer triangles
		




	Using triangles (rather than points) allows us to fill in the areas.


Drawing a Triangle

void triangle(GLfloat *a, GLfloat *b, GLfloat *c) {
   glVertex2fv(a);
   glVertex2fv(b);
   glVertex2fv(c);
}

Notes:

	A single  glBegin(GL_TRIANGLE) is done once (elsewhere)
	
Each time a third vertex is specified, a triangle is created


Splitting/Dividing a Triangle

void divide_triangle(GLfloat *a, GLfloat *b, GLfloat *c, int m) {	// m controls the recursion
   GLfloat v0[2], v1[2], v2[2];
   int j;
   if(m>0) {
      for(j=0; j < 2; j++) { 
         v0[j]=(a[j]+b[j])/2;
         v1[j]=(a[j]+c[j])/2;
         v2[j]=(b[j]+c[j])/2;
      }
      divide_triangle(a, v0, v1, m-1);
      divide_triangle(c, v1, v2, m-1);
      divide_triangle(b, v2, v0, m-1);
   }
   else 
      triangle(a,b,c); /* draw triangle at end of recursion */
}


Moving to Three Dimensions


		Again, can use midpoint method, or recursively subdividing tetrahedra

 


Using midpoint method


		Four vertices to randomly choose from
		
Three coordinates per vertex now
		
Must use glOrtho 
		
Use color to get some sense of depth

		for (GLint i = 0; i < 10000; i++) {
   int whichV = rand() % 4;
   GLfloat newPx = (px + vx[whichV]) / 2;
   GLfloat newPy = (py + vy[whichV]) / 2;
   GLfloat newPz = (pz + vz[whichV]) / 2;
   glColor3f (newPx, newPy, newPz);
   glVertex3f(newPx, newPy, newPz);
   px = newPx;
   py = newPy;
   pz = newPz;
}
		
Subdividing Tetrahedra

 

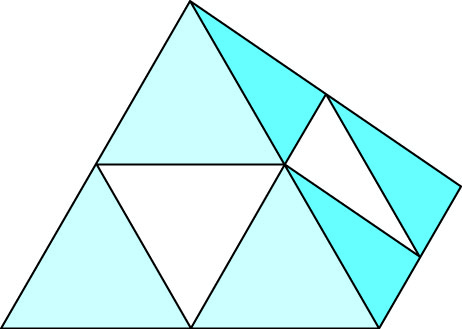
		Six midpoints
		
Recursivly subdivide four outer tetrahedra
		 		void divide_tetra(GLfloat *a, GLfloat *b, GLfloat *c, GLfloat *d, int m) {

   GLfloat v0[3], v1[3], v2[3], v3[3], v4[3], v5[3];
   int j;
   if(m>0) {
      for(j=0; j<3; j++) {
         v0[j]=(a[j]+b[j])/2;
         v1[j]=(a[j]+c[j])/2;
         v2[j]=(a[j]+d[j])/2;
         v3[j]=(b[j]+c[j])/2;
         v4[j]=(c[j]+d[j])/2;
         v5[j]=(b[j]+d[j])/2;
      }
			
      divide_tetra(a, v0, v1, v2, m-1);
      divide_tetra(v0, b, v3, v5, m-1);
      divide_tetra(v1, v3, c, v4, m-1);
      divide_tetra(v2, v4, v5, d, m-1);
   }
   else 
      tetra(a, b, c, d); /* draw triangle at end of recursion */
}
 				 
		
When at end of recursion, draw tetrahedron
			
				Draw four triangle faces using different color per face
			
			void tetra( GLfloat *a, GLfloat *b, GLfloat *c, GLfloat *d) {
    glColor3f(1, 0, 0);
    triangle(a, b, c);
    glColor3f(0, 1, 0);
    triangle(a, c, d);
    glColor3f(0, 0, 1);
    triangle(a, d, b);
    glColor3f(1, 0, 1);
    triangle(b, d, c);
}			
			
		
Want to perform hidden surface removal

		 
			
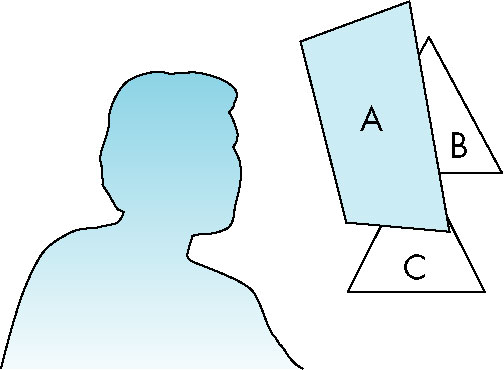
				Actually want OpenGL to do it
				
Must:
					
							Specify we want to use a z or depth buffer (part of the frame buffer)
							   glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);   //  typically in main
							   							
							
Enable z buffer algorithm 
						     glEnable(GL_DEPTH_TEST);   // main or init
						     
							
Clear z buffer upon redisplay
						     glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);   
						     
					
		

				
										



							


	
Code for Chapter 2

GL_POINTS	Vertices form individual points
GL_LINES	Vertices form pairwise line segments
GL_LINE_STRIP	Adjacent vertices are connected (polyline)
GL_LINE_LOOP	Same as LINE_STRIP, but sequence is closed-- i.e., last and first vertices are connected

i	integer
f	float
d	double

CISC 3620 Computer Graphics Chapter 2

Two-D Applications

A First OpenGL Program - The Sierpinski Gasket

Moving to an Actual Implementation

A C++/OpenGL Implementation of the Above

A 'Thirty-Second' Overview of the Above

Vertices

The OpenGL GLVertex Function

Specifying an Object as a Sequence of Vertices

Basic Structure of an OpenGL Program

The Graphics Systems vs User Interaction

The Display Callback Function

Coordinate Systems

OpenGL API

(Finite) State Machines

OpenGL Interface

Primitives

Approximating a Sphere

Text

Curved Objects

Attributes

Viewing

Aspect Ratio and Viewports

Revisiting the Gasket

Moving to Three Dimensions

Code for Chapter 2

CISC 3620
Computer Graphics
Chapter 2

The OpenGL `GLVertex` Function