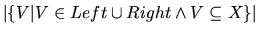m =
The constraint all_distinct(L) holds if variables in L are pair-wisely different. One naive way of implementing this constraint is to generate binary inequality constraints between all pairs of variables in L. This implementation has two problems: First, the space required to store the constraint is quadratic in the number of variables in L; second, splitting the constraint into small granularity ones may lead to the loss of possible propagation opportunities.
To solve the space problem, we define all_distinct(L) in the following way:
all_distinct(L):-all_distinct(L,[]).
all_distinct([],Left).
all_distinct([X|Right],Left):-
outof(X,Left,Right),
all_distinct(Right,[X|Left]).
delay outof(X,Left,Right):- dvar(X) : {ins(X)}.
outof(X,Left,Right):-true : outof(X,Left),outof(X,Right).
For each variable X, let Left be the list of variables to
the left of X and Right be the list of variables to the
right of X. The predicate call outof(X,Left,Right) holds
if X appears in neither Left nor Right. Instead of
generating inequality constraints between X and all the
variables in Left and Right, the call
outof(X,Left,Right) delays until X is instantiated. After
X becomes an integer, the calls outof(X,Left) and
outof(X,Right) exclude X from the domains of the variables in
Left and Right. It is not difficult to understand that
this implementation only consumes linear space.
In terms of the propagation ability, the second implementation is the same as the first one. In some systems, consistency checks are done to detect failure as early as possible. It is very easy to introduce consistency checks into the implementation. To do so, we only need to define outof(X,Left,Right) as follows:
delay outof(X,Left,Right):- dvar(X) :
{dom(X),min(X),max(X),ins(X)},
consistency_check(X,Left,Right).
outof(X,Left,Right):-true : outof(X,Left),outof(X,Right).
where consistency_check(X,Left,Right) does the consistency
check. There are many possible algorithms. The one implemented in
B-Prolog is as follows: Let n =If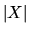
m =