Q-1: For each of the following statements, either prove it is true or give a counterexample.
- If P(a | b,c) = P(b | a,c), then P(a | c) = P(b | c).
- If P(a | b,c) = P(a), then P(b | c) = P(b).
- If P(a | b) = P(a), then P(a | b,c) = P(a|c).
Q-2: Consider the set of all possible five-card poker hands dealt fairly from a standard deck of fifty-two cards.
- How many atomic events are there in the joint probability distribution (i.e., how many five-card hands are there)?
- What is the probability of being dealt a royal straight flush? a stright flush? a stright?
- What is the probability of being dealt a full house (three of a kind and two of another kind)?
Q-3: Consider the following full joint distrubition:
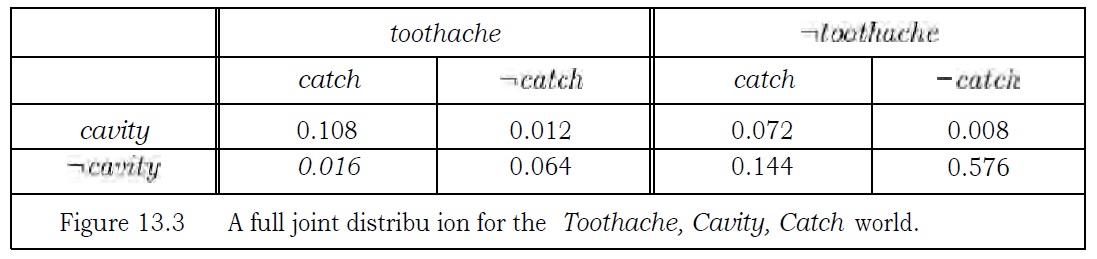
calculate the following:
- P(toothache)
- P(Cavity)
- P(Toothache | cavity)
- P(Cavity | toothache \/ catch)
Q-4: Consider two medical tests, A and B, for a virus,
Test A is 95% effective at recognizing the virus when it is present,
but has a 10% false positive rate (indicating that the virus is
present, when it is not). Test B is 90% effective at recognizing the
virus, but has a 5% false positive rate. The two tests use independent
methods of identifying the virus. The virus is carried by 1% of all
people. Say that a person is tested for the virus using only one of the
tests: and that test comes hack positive for carrying the virus. Which
test returning positive is more indicative of someone really carrying
the virus? Justify your answer mathematically.
