Logic Gates: NAND
The NAND (= "not and") logic gate takes two bits as an input. Its output follows the rule: "as long as the bits aren't both $1$ (that is, if at least one of the bits is $0$,) output $1$; otherwise, output $0$." You can implement it in your code as follows: given the Boolean variables x and y, then !(x && y) means "x nand y". Below is the black-box representation of the NAND gate and its truth table.
Bonus question: How can we build a NAND gate if we know how to build NOT, AND, OR, and XOR gates?
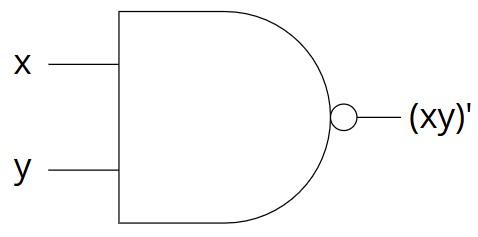
NAND Gate: black-box representation. Miriam Briskman, CC BY-NC 4.0.
| Input | Output | |
|---|---|---|
| x | y | (xy)' |
| $0$ | $0$ | $1$ |
| $0$ | $1$ | $1$ |
| $1$ | $0$ | $1$ |
| $1$ | $1$ | $0$ |
These notes by Miriam Briskman are licensed under CC BY-NC 4.0 and based on sources.