Logic Gates: XNOR
The XNOR (= "not exclusive or") logic gate takes two bits as an input. Its output follows the rule: "if both bits are the same, output $1$; otherwise, output $0$." You can implement it in your code as follows: given the Boolean variables x and y, then !(x ^ y) means "x xnor y". Below is the black-box representation of the XNOR gate and its truth table.
Bonus question: How can we build an XOR gate if we know how to build NOT, AND, OR, XOR, NAND, and NOR gates?
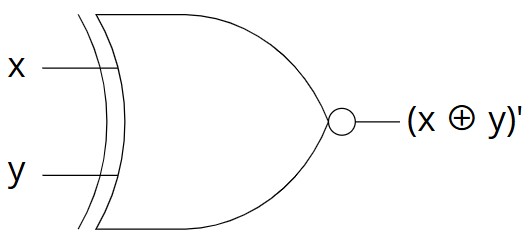
XNOR Gate: black-box representation. Miriam Briskman, CC BY-NC 4.0.
| Input | Output | |
|---|---|---|
| x | y | (x ⊕ y)' |
| $0$ | $0$ | $1$ |
| $0$ | $1$ | $0$ |
| $1$ | $0$ | $0$ |
| $1$ | $1$ | $1$ |
